扇形の弧の長さと面積 扇形の弧の長さと面積を求める問題です。 まずは、中心角から、扇形が円に対してどのくらいの割合なのか(何倍なのか)を求める事が大事です。 公式を覚えて当てはめるだけの練習だと、あとあと意味側からなくて苦労します。面積を求めよ。 半径4cm、中心角75°のおうぎ形がある。 弧の長さを求めよ。 面積を求めよ。 半径 18 5 cm, 中心角125°のおうぎ形がある。 弧の長さを求めよ。 面積を求めよ。 半径8cm, 中心角405°のおうぎ形がある。 弧の長さを求めよ。 面積を求めよ。④ 側面の扇形の中心角は, r R ×360° 問題2 右の図の円錐の表面積を求めよ。 解 側面の扇形の中心角をa° とすると, 2∏×8× a 360 =2∏×4,a=180。展開図は右下のようになる。 側面積∏×× 180 360 =32∏ (cm2),底面積∏×42= 16∏ (cm2)
扇形进阶 容斥原理有关的面积题 哔哩哔哩 つロ干杯 Bilibili
扇形 面積 問題
扇形 面積 問題-1 直径8の円の上半分の面積 直径が8だから半径は4.半円だから円の面積の半分:4 2π ÷2=8 π π 採点する やり直す 解説 2 半径 6 ,中心角が1°の扇形の面積 1°だから円(360°)の3分適度な難易度の面積の問題を90問集めました。 1ページ3問ずつで,式や筆算を書き込むスペースが十分あるので大変学習しやすくなっています。 また,解答解説はこれ以上ありえない位くわしく書いてあります。 面積の問題のPDFはこちら↓↓ 面積の問題



扇形面積題庫面積和體積 二 Jkveno
「圓心角」。扇形可視為圓的一部分。將扇形與分數結合(幾分之幾圓)。能畫出指定扇形。 學習表現: sⅢ2 認識圓周率的意義,理解圓面積、圓周長、扇形面積與弧長之計算方式。 議 題: 閱讀素養教育 核心素養: 系統思考與解決問題 更新時間: 円と扇形問題の解き方 おうぎ形はどこに? (中学受験算数 標準問題 気づかなかった問) どう分ける? (中学受験算数 面積分割) 面積は? (中学受験算数 平面図形) どんな工夫をする? (中学受験算数 平面図形)おうぎ形面積の基本問題(東海中学 10年) 円周率が3より大きいことがわかる作図(逗子開成中学 09年) 計算の仕方が試される問題(雙葉中学 13年) よく使われる題材の面積問題(大阪星光学院中学 10年改題)
求扇形弧長與面積。知道以下三個比相等:(1)圓心角:360;(2)扇形弧長:圓周長;(3)扇形面積:圓面積,但應用問題只處理用(1)求弧長或面積。 學習表現: sⅢ2 認識圓周率的意義,理解圓面積、圓周長、扇形面積與弧長之計算方式。 議 題: 閱讀求める面積は左図のχの部分 つまり、正方形から a,b,c,dの4カ所を ひいてやれば良いことが分かる! a,b,c,d は合同なので a の面積だけの求め方を考える! a の部分の面積を求めるには左図の手順でよい! (扇形の面積)=π(10) 2扇形の面積を求める公式は、次の通りです。 S = πr2 × x 360 = 1 2lr S = π r 2 × x 360 = 1 2 l r 中心角 x°、半径 r の扇形 ここで、S は扇形の面積、π は円周率、r は円の半径、x は中心角(単位「度」)を
おうぎ形面積の基本問題(東海中学 10年) 円周率が3より大きいことがわかる作図(逗子開成中学 09年) 計算の仕方が試される問題(雙葉中学 13年) よく使われる題材の面積問題(大阪星光学院中学 10年改題)中学受験 算数の練習問題プリントです。栄光ゼミナールの約7万名の生徒が自宅や教室で毎日挑戦している問題データベースから、定番の問題を集めて公開しています。 中学受験 算数プリントの主な内容 和差算 植木算 周期算 分配算 方陣算 展開図と見取図 等差数列のしくみ 円と多角形 割合側面積(扇形の面積)は,π×× nnn = 16 π 底面積と側面積(扇形の面積)を加えると,表面積は π (2) 底面は半径 3 の円だから,底面積は π×32= 9 π 展開図において扇形の中心角を x° とおくと,扇形の弧の長さが底面の円周の長さと等しくなる



圆弧面积计算公式图解 图片欣赏中心 急不急图文 Jpjww Com



Q Tbn And9gcqpqxxknzceay3mjcxzcklaz Iozcfat84mkqdgzflcwlamy23 Usqp Cau
ソフト詳細説明 このプログラムは、扇形の面積を求める問題を、次々と作成することができます。 もちろん、解答付プリントも印刷できます。 その求め方の解説も付いています。 おもしろ問題1問目! 一番内側の円に内接する正方形の面積はいくつ? 解説 おもしろ問題2問目! どちらのチーズタルトの面積が大きい? 解説 おもしろ問題3問目! 茶色い半円と余白部分、どちらが大きい? 解説問題16 図の黒い部分の面積は24c㎡です。外側の正六角形の面積を求めなさい。 → 解答 問題17 たて10cm、よこ15cmの長方形の中に半径2cmの円があります。この円が長方形の内側をまわりにそって回るとき、円の通らない部分の面積を求めなさい。



阴影面积问题 之十




09 11 27 01 圓與扇形 不學無數 隨意窩xuite日誌
まとめ:扇形の面積は「おうぎ形パワー」を円にかける 扇形の面積の求め方はどうだった? ? 円の公式に毛がはえたようなもんだから、頑張れば覚えられそうだね。 S = πr² × α / 360 「円とおうぎ形」がテストにでるときに確認したいね^^ おうぎ形の 問題文に面積が与えられているので、円と扇形の面積を比較しながら中心角を求めます。 半径が4㎝の円の面積は、\(\pi\times 4^2=16\pi(cm^2)\) 半径が4㎝の扇形の面積は、問題文より \(4\pi(cm^2)\) です。Weekend Mathematics/問題/問題93 93.おうぎ形の面積 下の図のような、半径がcm、中心角が144°のおうぎ形があります。 点エ、オ、カ、キ、ク、ケ、コは、おうぎ形の弧イウ(曲線の部分イウ)を 8等分する点です。




圓的周長與面積 27 扇形的複合圖行計算2 Youtube




葉子問題帶來的思考 好玩的數學課 隨意窩xuite日誌
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators扇形 以下の問いに答えなさい。ただし、円周率はˇ とする。 (1) 半径2cm、中心角90 °の扇形の面積と弧の長さを求めなさい。 (2) 半径3cm、中心角60 °の扇形の面積と弧の長さを求めなさい。 (3) 半径6cm、中心角1 °の扇形の面積と弧の長さを求めなさい。 (4) 半径4cm、中心角45 °の扇形の面積と 図形の面積を求める問題ですね。 こちらも中学受験問題の定番です! この辺りも昔と変わっていませんね! 問題を読むと三角形CDEの面積は96cm2とあります。 つまり辺CDからEまでの高さが問題を解く上でキーになりそうなこと予想できますね。




湖南省九年级数学上册第二十四章圆24 4 弧长和扇形面积 1 教案新人教版下载 Word模板 爱问共享资料




九年级上册第二十四章圆弧长和扇形面积 第2课时 北京市十一学校李鹏飞 Ppt Download
高中選修數學乙(上) 21 弧度、弧長 2 (1) s=rθ。 (2) A= 1 2 r2θ= 1 2 rs。 2 特別注意,在使用這兩個公式時,θ 都要先化為弧度。 例題2 求扇形的弧長與面積 由一圓弧與一弦所圍成的區域稱為弓形。扇形の面積の和から正方形をひく 正方形と扇形の面積をつかった問題がわかる3ステップ 例題をといてみよう。 例題 つぎの図形における緑の斜線部の面積を求めなさい。おうぎ形の面積 = 半径 × 半径 × π × 中心角 360° より 面積 =9×9×π× 64 360 = 72 5 π 答 72 5 π cm 2 確認問題 次の問いに答えよ。 半径6cm, 中心角30°のおうぎ形の弧の長さを求めよ。 cm ☓ π 半径3cm, 中心角80°のおうぎ形の面積を求めよ。




问题 如图 扇形oab半径为2 Ob 3 求阴影部分的面积 小升初 好题网



长沙小升初奥数几何问题之圆与扇形解题方法 苏州景观工程有限公司
小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題扇の面積を使った応用問題 扇の面積を使った応用問題にチャレンジしてみましょう。 次の図形は、1辺が4cmの正方形の中に扇が組み合わさったものである。斜線部分の面積を求めよ。 ポイント ABCの面積をもとめるために、「正方形OABCから扇OA




正方形内一个半圆一个扇形 在一个正方形里有一个半圆和一个扇形 2c求扇形和半圆的阴影部分的面积 三人行教育网 Www 3rxing Org




一道小學六年級數學題 中學老師幾天幾夜做不出來 問題出在哪 壹讀




名師學院數學精英班主題15 圓 扇形周長特訓9 齊峻老師 扇形面積難題



數學 圓形面積 現在的國小課本應該沒有擺這一個深入題了吧 Sanmoelen的創作 巴哈姆特




解題方法 陰影部分面積的必備方法 每日頭條




Asep教材組國二數學四扇形重疊 花蕊 面積題 Youtube




常用圖形求面積計算公式 人人焦點



扇形面积计算进阶 腾讯视频




正方形里有两个扇形圆求阴影面积 边长为1的正方形内 两个扇形 一个半圆 求阴影面积 三人行教育网 Www 3rxing Org




小六資優複習影片7 複合圖形1 Youtube




小學陰影面積要計算 難倒一批英雄漢 家長高呼 請放過我的孩子 每日頭條




小六資優數學選粹題15 扇形面積活用asepx凱爺數學 Youtube




扇形面積扇形面積在線計算器 Lhlv




小學數學面積問題的幾種常見題型彙編 每日頭條



扇形面积计算 西瓜视频搜索




18年中考數學百日衝刺快速提分祕籍 破解 有關圓的計算的技巧 Itw01



扇形面积问题 初三 数学作业 移商院




扇形与正方形重叠阴影面积 正方形边长为 一个半圆和扇形重叠阴影部分a 求a的面积 三人行教育网 Www 3rxing Org




這道競賽題求圖形的面積差 題目難出新高度 只有尖子生能做對 人人焦點



中考数学 扇形中两个半圆 求不规则阴影的面积 方法多多啊 哔哩哔哩 つロ干杯 Bilibili



1
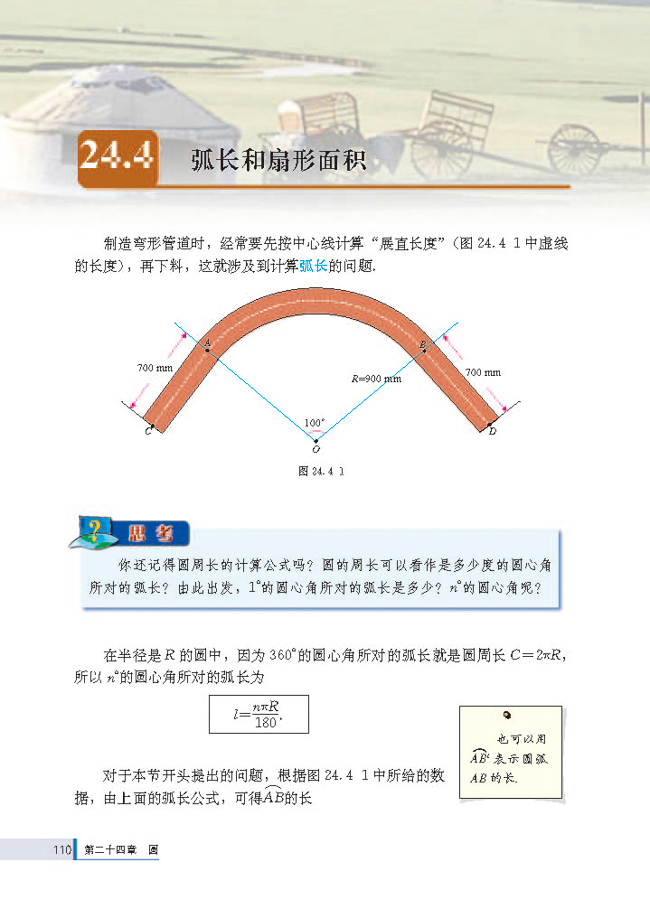



24 4弧长和扇形面积 人教版九年级数学上册 初中课本 中学课本网
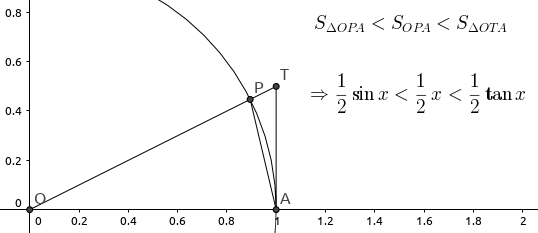



圆的面积凭什么是pr Li Hua 博客园




扇形的周长和面积 求扇形的面积和周长公式 三人行教育网 Www 3rxing Org



1



和扇形有关的简笔画 和扇形有关的简笔画画法



典例精析 一 基础知识题型 例1 如图24 4 5 边长为1的菱形abcd绕点a旋转 当b C两点恰好落在扇形aef的弧ef上时 弧bc的长度等于 图24 4 5 A B C D Jx 要求弧bc的长度 关键是求弧bc所对的圆心角 这由菱形的性质和圆的半径关系可得 连接ac 由




網友的數學問題 耕圃莘園 隨意窩xuite日誌
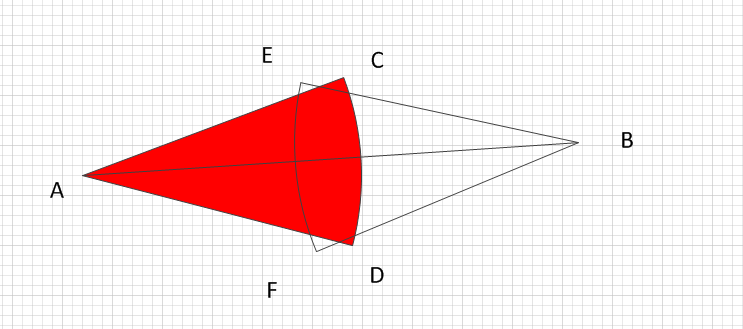



求两个扇形的重叠面积 Python Csdn问答




年中考数学必考专题26与弧长 扇形面积有关的问题 原创版 七七文库www 77wenku Com



扇形面积教育 腾讯视频




數學題目求解 Mobile01




小學陰影面積要計算 難倒一批英雄漢 家長高呼 請放過我的孩子 每日頭條




题集 几何 求阴影部分面积 李宣 S 数学博客



私校資優數學 面積題目 扇葉形狀 Nova的科學反主流學院




圓的周長與面積 26 扇形的複合圖行計算1 Youtube



初三数学题关于扇形 三角形的面积的问题 图片欣赏中心 急不急图文 Jpjww Com




问题 如图 在扇形内白色区域是一个面积为25平方厘米的正方形 求阴影部分的面积 好题网



阴影面积问题 之十




圓面積 圓 是一種規則的平面幾何圖形 圓面積就是指圓形所占的平面空間大小 百科知識中文網




圓面積公式 圓是最重要的曲邊形 古埃及人把它看成是神賜予人的神聖圖形 圓 百科知識中文網



阴影面积问题 之十



技巧 数学图形面积计算的十种方法




扇形の面積の求め方 公式と計算例
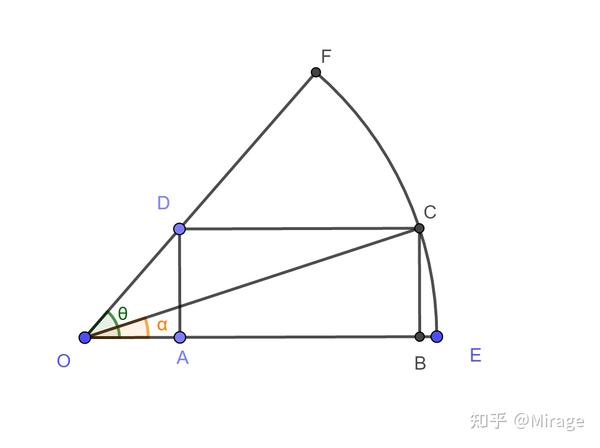



扇形内接矩形问题 知乎



奧數揭秘 直角三角形與扇形 香港文匯報



扇形进阶 容斥原理有关的面积题 哔哩哔哩 つロ干杯 Bilibili




數學題目求解 Mobile01




一般 複合圖形的面積 數學 均一教育平台




幾何題目其實挺好玩的 主要是思路要靈活 三到六年級 趣讀



一個複雜的面積問題 4個四分之一的圓和正方形重疊 王哲國小資優數學 隨意窩xuite日誌



初三数学题关于扇形 三角形的面积的问题 图片欣赏中心 急不急图文 Jpjww Com




例題 扇形的複合圖形計算2 數學 均一教育平台




年中考数学必考专题26与弧长 扇形面积有关的问题 原创版 七七文库www 77wenku Com




九年級數學 陰影部分面積 這種題目很常見 每日頭條
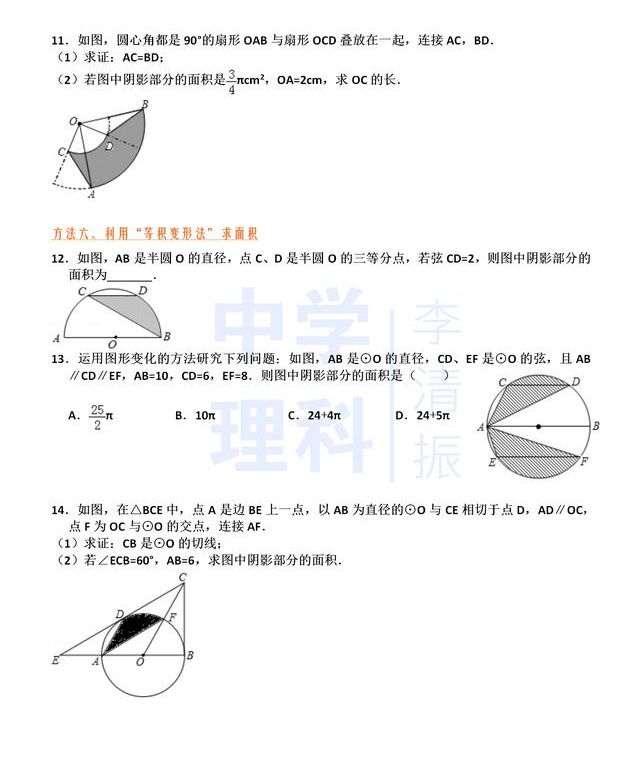



原创 六大方法巧求中考数学与圆有关的面积问题 错过可惜 今日焦点




小六學藝競賽數學科考題14 扇形面積問題凱爺數學 Youtube



圆弧面积计算公式图解 图片欣赏中心 急不急图文 Jpjww Com



如何求扇形面积 西瓜视频搜索



扇形面積題庫面積和體積 二 Jkveno



浅析弧长和扇形面积计算问题 中国期刊网




正方形面積計算正方形面積 Wjklv




24 4 1弧长和扇形面积教学设计下载 Word模板 爱问共享资料




不等边扇形算面积 如何求两边不等扇形的面积 三人行教育网 Www 3rxing Org



年中考数学必考专题26与弧长 扇形面积有关的问题 原创版 七七文库www 77wenku Com




數學面積計算過程中常見的重疊問題及計算 每日頭條



小学数学 图形求面积 的10大解题方法 很实用 新闻频道 手机搜狐



正方形扇形面積正方形と扇形の面積をつかった問題がわかる3ステップ Jkveno




扇形面積8 扇形面積 百度百科 Mqttk



初三数学题关于扇形 三角形的面积的问题 图片欣赏中心 急不急图文 Jpjww Com



六年级几何问题圆与扇形例题讲解 巧求面积 奥数网



小学数学 30道小升初几何问题 答案 孩子吃透 考试不丢分 小初高题库试卷课件教案网




初三数学上册 弧长和扇形面积 教学ppt课件 牛图文



私校資優數學 面積題目 扇葉形狀 Nova的科學反主流學院



私校資優數學 面積題目 扇葉形狀 Nova的科學反主流學院



弧度制下的扇形问题 1 1任意角的概念与弧度制 高中人教b版 数学中国网




年中考数学必考专题26与弧长 扇形面积有关的问题 原创版 七七文库www 77wenku Com



私校資優數學 面積題目 扇葉形狀 Nova的科學反主流學院




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく




扇形の弧の長さと面積 計算ドリル 問題集 数学fun




18年中考數學百日衝刺快速提分祕籍 破解 有關圓的計算的技巧 Itw01



扇弧形面积的计算方法 西瓜视频搜索
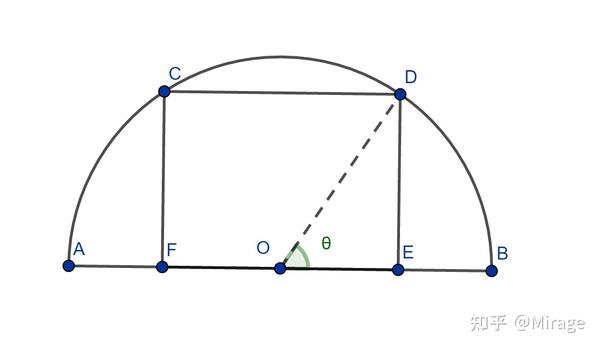



扇形内接矩形问题 知乎



扇形的面积 教案 教师资格面试初中数学 中公教育网




知识 与圆的有关计算之扇形的有关计算 Math实验室



弧长和扇形面积 圆ppt 第一课时 第一ppt



初中數學幾何陰影面積的三種解法 初中生趕緊收藏 Zi 字媒體



初中數學幾何陰影面積的三種解法 初中生趕緊收藏 Zi 字媒體




小学阴影面积题大全



有問有答



小学奥数五六年级面积问题 两个扇形拼正方形 这种算法你会吗 网易视频



Q Tbn And9gctfuio0fq9nrv8vuy22h 2ys6tktt4a8mnall Dw1fvs D356x7 Usqp Cau




小學數學思維訓練 圖形陰影面積計算常見題型全面分析 每日頭條



數學 圓形面積 現在的國小課本應該沒有擺這一個深入題了吧 Sanmoelen的創作 巴哈姆特



0 件のコメント:
コメントを投稿