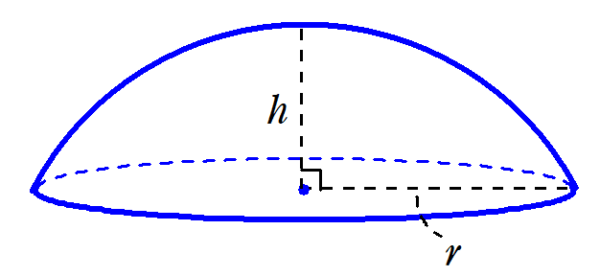
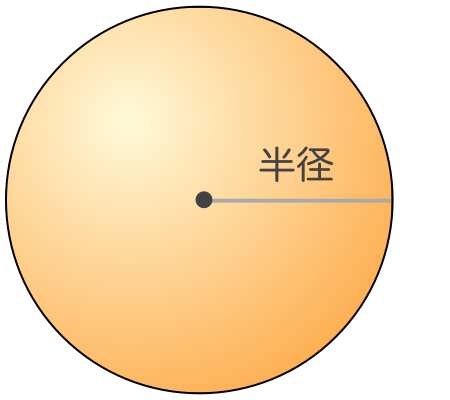
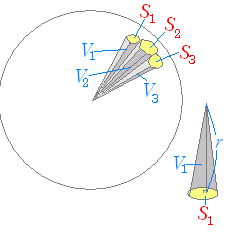
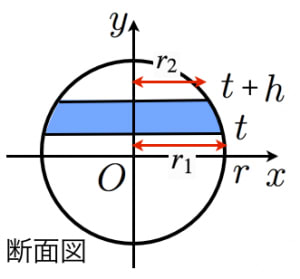
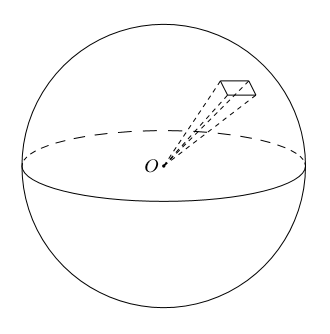
3.球の体積を求める方法 球の体積は、小さな三角錐に近い形をしたものを足し合わせていくと求めることができます。 下の図を見てください。 この図は、球を三角錐の集まりにした図です。rとは半径
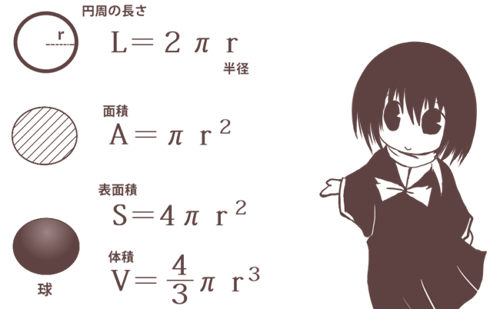
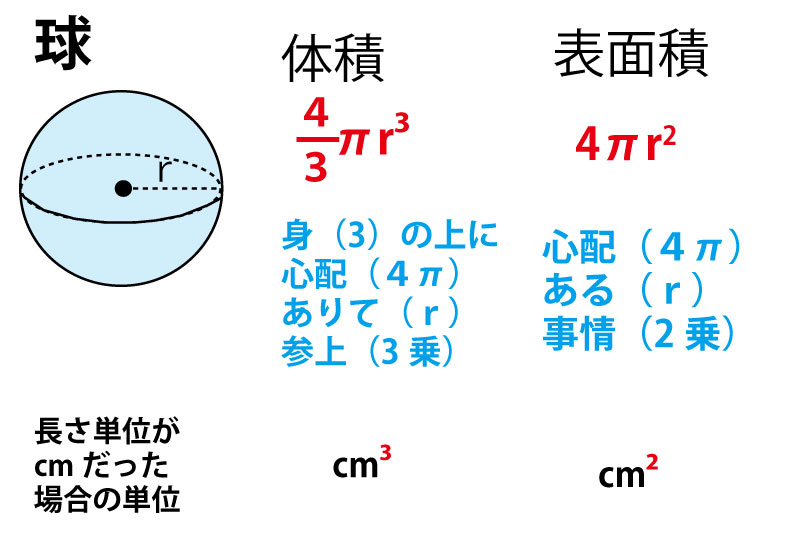
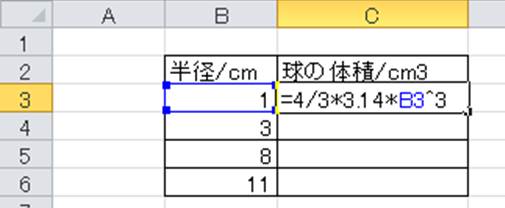
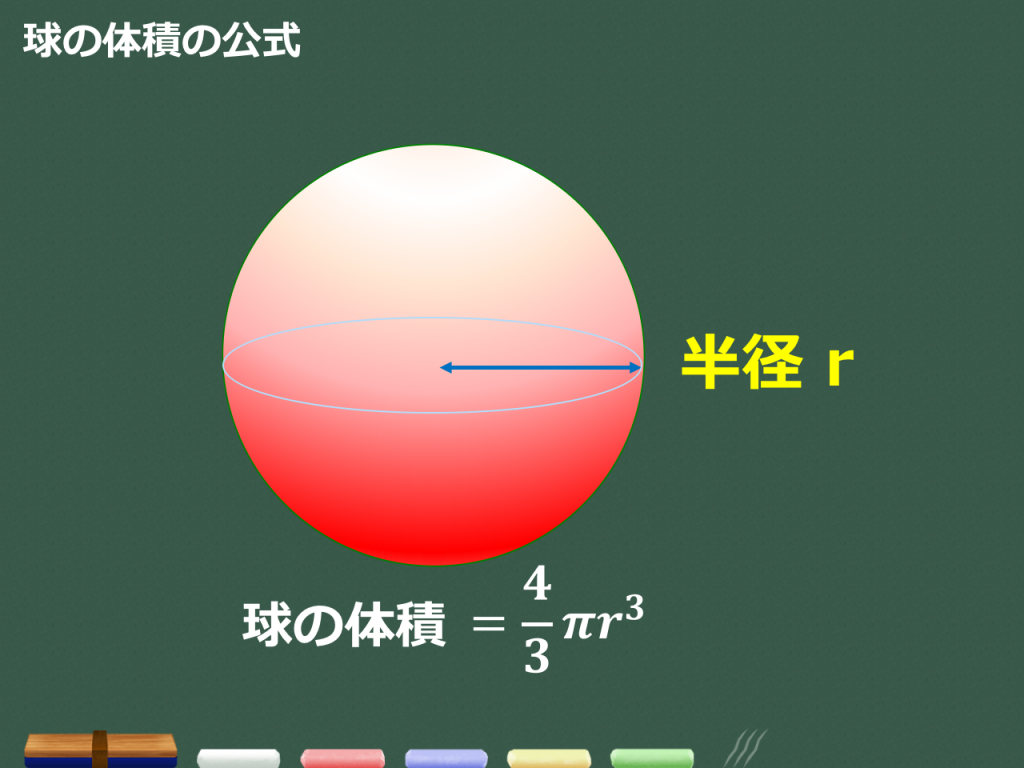
球 体積 求め方 重積分-の体積 V = 4 3πr3 V = 4 3 π r 3 体積 = 4 × 314 × 半径 × 半径 × 半径 ÷ 3 公式の 導出 ( どうしゅつ ) 方法と計算例は、「 球の体積の求め方 」をご覧ください。 球の体積の求め方球 ボール 体積計算 公式 求め方 計算方法 直径 半径 自動 円周率 volume
球 体積 求め方 重積分のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
 |  |  |
「球 体積 求め方 重積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「球 体積 求め方 重積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 | ||
「球 体積 求め方 重積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「球 体積 求め方 重積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 | ||
「球 体積 求め方 重積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
「球 体積 求め方 重積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  | |
「球 体積 求め方 重積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  |  |
「球 体積 求め方 重積分」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
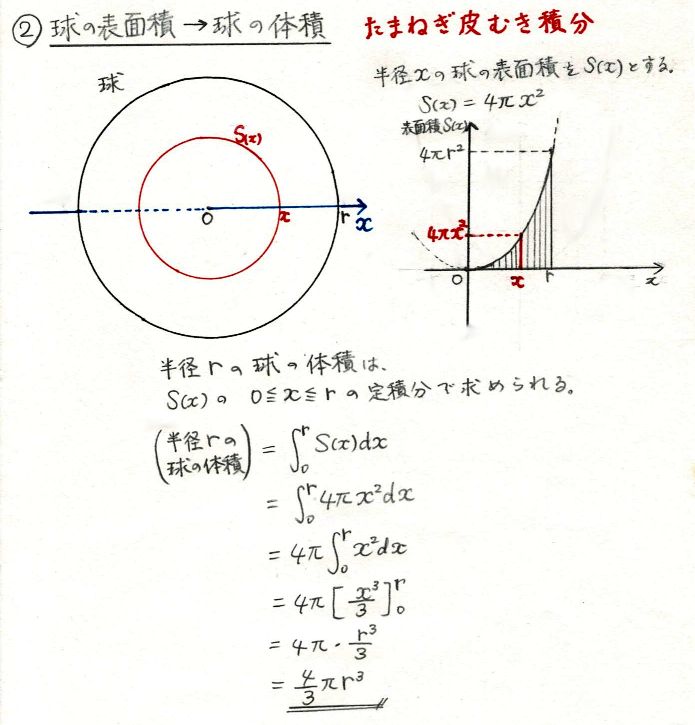 | 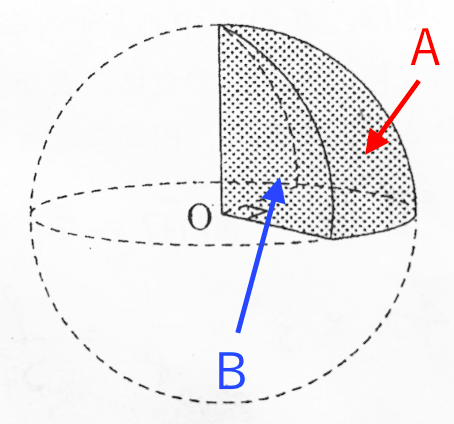 |
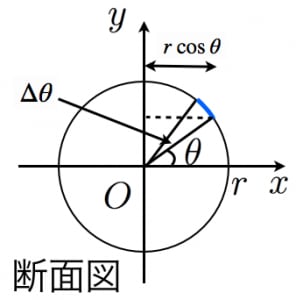
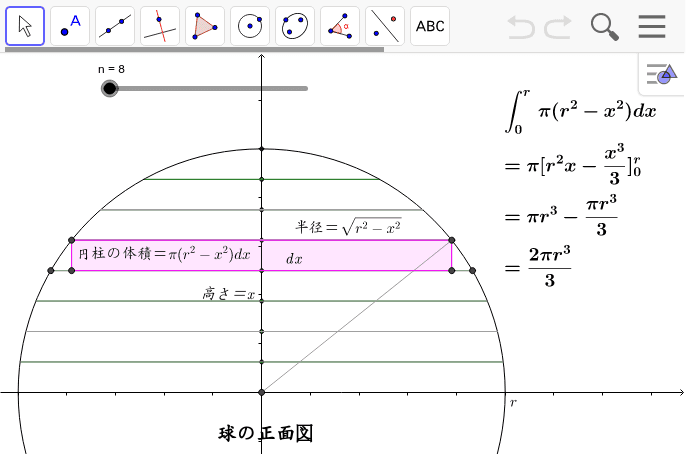
求め方2:球体の体積を用いる方法 求め方1:微小の範囲を考える方法 考え方 青い部分の面積 を考える. 幅は 、長さは なので, より微小な角度を考える 球全体で積分する 計算 求め方2:球の体積を用いる方法 考え方 半径 の球の表面積を とおく楕円の面積と楕円体の体積の求め方 korokoro 年10月7日 こんにちは( @t_kun_kamakiri )。 さてこの記事を読みに来た方は、「楕円の面積や体積の公式」を求めてきたことだと思います。 あるいは、楕円の面積や体積の公式はどうやって導かれるのかと知り
Incoming Term: 球 体積 求め方, 球 体積 求め方 重積分, 球 体積 求め方 原理, 球 体積 求め方 積分, 球 体積求め方 例題,




0 件のコメント:
コメントを投稿